7.17 组会

Chaitanya K. Joshi, Thomas Laurent, and Xavier Bresson. "An Efficient Graph Convolutional Network Technique for the Travelling Salesman Problem.", Computing Research Repository abs/1906.01227 (2019)

和 中的一样，神经网络的输出 表示该边在图的最优解中的概率，损失函数为 和最优解的交叉熵损失，即为将问题看作为一个分类问题。

得到 后，通过束搜索来求解问题。

Wouter Kool, Herke van Hoof, and Max Welling. "Attention, Learn to Solve Routing Problems!", arXiv: Machine Learning (2019)

文章由 提出了一个基于注意力层的模型，并用 算法来训练模型。

将 问题的解定义为 ，是节点的一个排列。基于问题实例 找到解 的随机策略：

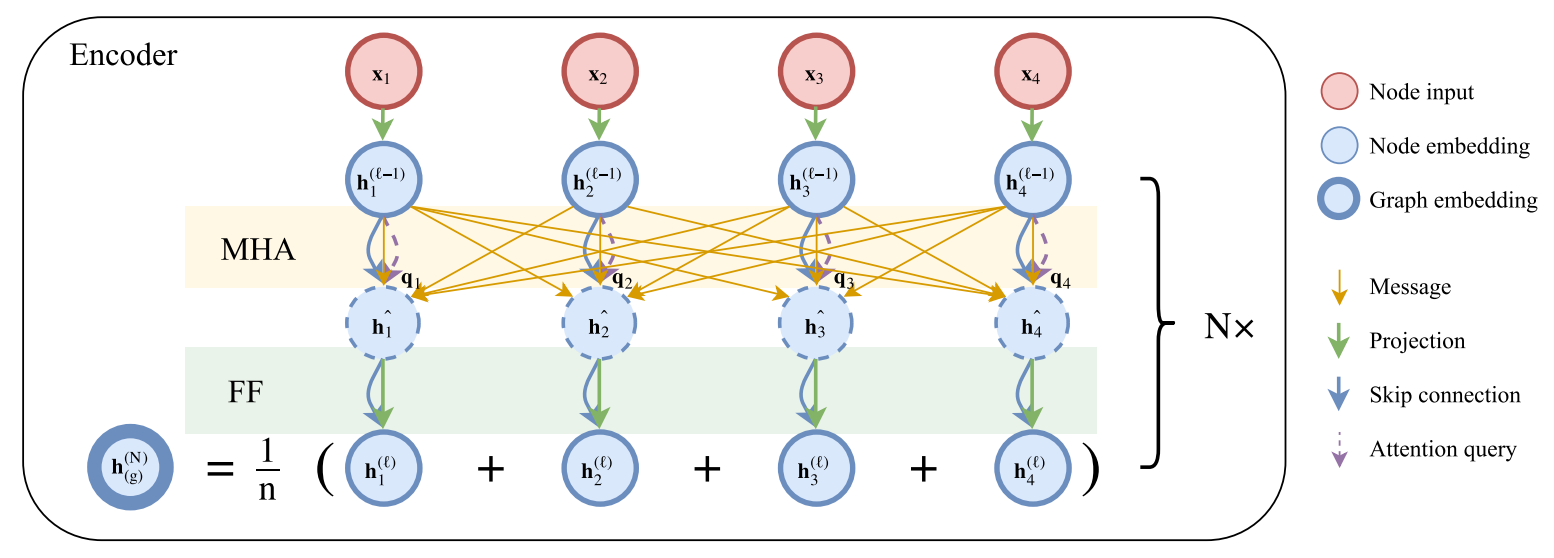
Encoder

没有采用位置编码，输入的节点无次序之分。

先将维度为 的节点坐标特征 嵌入到维度为 的向量 中： 然后 通过 层注意力层来更新（实验中 ），类似于 ，注意力层每一层包含两个子层，一个 头注意力层（）和一个全连接层（），每个子层中还有残差链接和批归一化： 通过 得到点嵌入 和图嵌入 ，都作为 的输入。

Attention mechanism

Multi-head attention

Feed-forward sublayer

Batch normalization

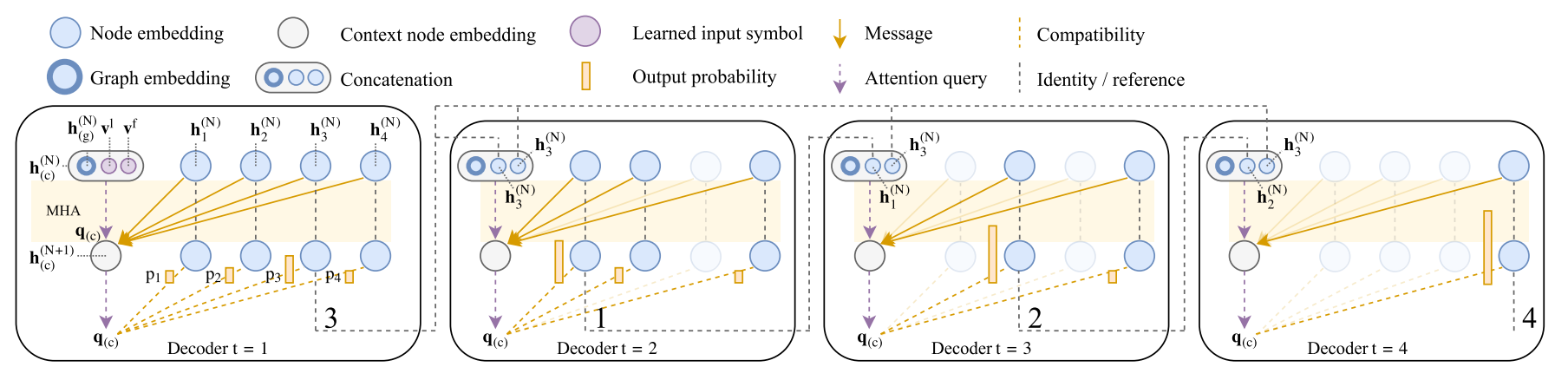
Decoder

由两层注意力层构成，一层多头注意力层，一层单头注意力，这里的注意力层没有采用残差连接、批归一化、全连接层操作，而是直接得到相关性分数。

： 在 时刻的输入来自 和 之前其本身的输出： 其中 和 是维度为 的学习到的参数。

将 和 计算： 然后和上面 中一样求出 头注意力层输出结果 。

最后用一个单头注意力层来求出输出概率 ，其中用 函数来将结果修正到 ：

Train

policy gradient

论文中的梯度计算公式为： 其中 是累计奖励函数，对于 即为路径长度。 是 ，减去 后能减少 的方差，利于梯度更新。

是采取采样策略， 的概率选择当前概率最大的点输出， 的概率随机选择一个点输出。

是采取贪心策略，每次都是选择当前概率最大的点输出。

当 和 两个分布差异很大时，则用 来更新 。