ML for CO | 刘皓铭

ML for CO 综述

Yoshua Bengio, Andrea Lodi, and Antoine Prouvost. "Machine learning for combinatorial optimization: A methodological tour d'horizon", European Journal of Operational Research 290.2 (2021): 405-421.

不失一般性的，CO 问题可以被公式化为一个受约束的最小优化问题。如果目标和约束是线性的，则该问题称为线性规划（LP）问题。如果一些变量也被限制为只能为整数值，则问题被称为混合整数线性规划（MILP）问题。可用单纯形算法多项式复杂度求解 LP 问题。

分支限界（branch and bound），分支是使用广度优先策略，依次生成扩展结点的所有分支，限界是在结点扩展过程中，计算结点的上界，搜索的同时剪掉某些分支。分支限界法就是把问题的可行解展开，再由各个分支寻找最佳解。

对于 MILP 问题，分支限界算法为将问题松弛为实数变量后分解为小问题。

End to end learning

通过 ML，由 Problem defifinition 直接得到 Solution。ML 适合在较短的计算时间内获得准确的解决方案，因为一些复杂性是在学习阶段离线解决的。

Learning meaningful properties of optimization problems

通过 ML，为传统的运筹优化方法提供信息。

Machine learning alongside optimization algorithms

构建 CO 算法，在整个执行过程中反复调用 ML 模型。主算法控制高级结构，同时经常调用ML模型以协助较低级别决策。

最大公共子图（MCS）

Ciaran McCreesh, Patrick Prosser, and James Trimble. "A Partitioning Algorithm for Maximum Common Subgraph Problems.", International Joint Conference on Artificial Intelligence (2017): 712-719.

Yanli Liu, Chumin Li, Hua Jiang, and Kun He. "A Learning Based Branch And Bound For Maximum Common Subgraph Related Problems", AAAI Conference on Artificial Intelligence 34. (2020): 2392-2399.

Jianrong Zhou, Kun He, Jiongzhi Zheng, Chu-Min Li, and Yanli Liu. "A Strengthened Branch and Bound Algorithm for the Maximum Common (Connected) Subgraph Problem", European Conference on Artificial Intelligence (2022): 1908-1914.

The McSplit Algorithm

搜索过程中的当前状态为点对的映射，同时将还未考虑的点打上一个与已考虑的点集连通性的，相同的点对才可加入映射，即选择处于同一标签类的点对。

当前状态对应的答案上界为：启发式：选择标签类时，选择最小的标签类，从中选点时，选度数最大的点。

McSplit+RL

因为预计的上界越小，越可能剪枝，因此考虑将上界的减少量作为奖励。
同时，若考虑上界的减少率，则又得到一种变体方法。
考虑点对的匹配作为奖励。

McSplit+LL Algorithm

Long-Short Memory (LSM)

随着搜索的深入，当前状态会有很大的变化，均匀地累积分数会导致由大部分历史评估值引起的偏差。因此，需要一种能够消除历史评估的影响的机制。

考虑短期阈值（默认为）和长期阈值（默认为）。若大于，则所有衰减到一半。若大于，则所有衰减到一半。

Leaf vertex Union Match (LUM)

叶节点定义为只跟一个点相邻的节点。一个点的叶子定义为与该点相邻的叶节点。

定理：在进行时，当一对点匹配时，可以从的不匹配的叶子中匹配尽可能多的点对，而不影响解的最优性。

旅行商问题（TSP）

LKH

求解 TSP 的启发式算法可分为三类：回路构造算法、回路改进算法和复合算法。复合算法通常使用回路改进算法对回路构造算法得到的初始解进行改进。LKH 算法是一种利用 k-opt 来改进启发式构造的初始行程的复合算法。

k-opt：替换当前解的条边，得到一个更优的新解。

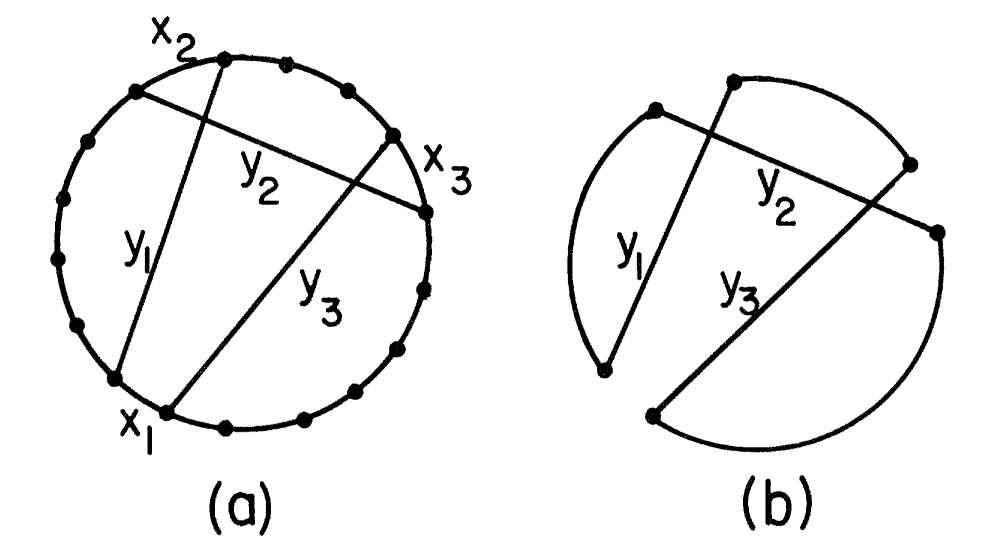
1-tree 下界：从中选出一个点，求出剩下点的最小生成树，最小生成树的权值再加上向最小生成树的不同两个点连出的最小权值的边的权值（一条边为进入最小生成树，一条边为离开最小生成树），即为 1-tree 下界。1-tree 下界不一定是可行解。当 1-tree 中每个点度数都为时为可行解，且为最优解。

定义，其中为 1-tree 的权值，为必须包含边的 1-tree 的权值。一条边的值可以看做必须包含该边的最小 1-tree 的额外权值。在 LKH 算法中，有更小的值的边在搜索中有更高的优先级。

Held-Karp 下界：LKH 算法通过添加惩罚来最大化最优 TSP 解的下界，边权变为：。这个变化不改变 TSP 的最优解，但改变了最小的 1-tree。最大化，即为 Held-Karp 下界。迭代为，其中为点在最小 1-tree 中的度数，为迭代的参数，为迭代的轮数。迭代即为让最小 1-tree 中的点的度数都变为。

VSR-LKH

Jiongzhi Zheng, Kun He, Jianrong Zhou, Yan Jin, and Chu-min Li. "Combining Reinforcement Learning With Lin-Kernighan-Helsgaun Algorithm For The Traveling Salesman Problem", AAAI Conference on Artificial Intelligence 35 (2021): 12445-12452.

VSR-LKH 中，k-opt 过程不再是遍历候选边集，而是通过强化学习来从候选边集选择添加的边。对于该强化学习，状态为当前需要加边的点，动作为加边，加边后状态转移为所加边的另一个端点，奖励为：定义的初始为：影响选择边的优先级。

NeuroLKH

Liang Xin, Wen Song, Zhiguang Cao, and Jie Zhang. "NeuroLKH: Combining Deep Learning Model with Lin-Kernighan-Helsgaun Heuristic for Solving the Traveling Salesman Problem.", Conference on Neural Information Processing Systems (2021): 7472-7483.

LKH 中迭代后能提升候选边集的质量，但仍有局限性，因此提出了 NeuroLKH 来构建候选边集。

首先将原图转化为稀疏有向图，每个点所连的边只保留最短的条，这条看作是该点连出的有向边。实验中取了。

用稀疏图网络来预测边的权值和点的惩罚。不是边权，其权值越大，搜索中越优先选择这条边，即为上面改变边权的惩罚。

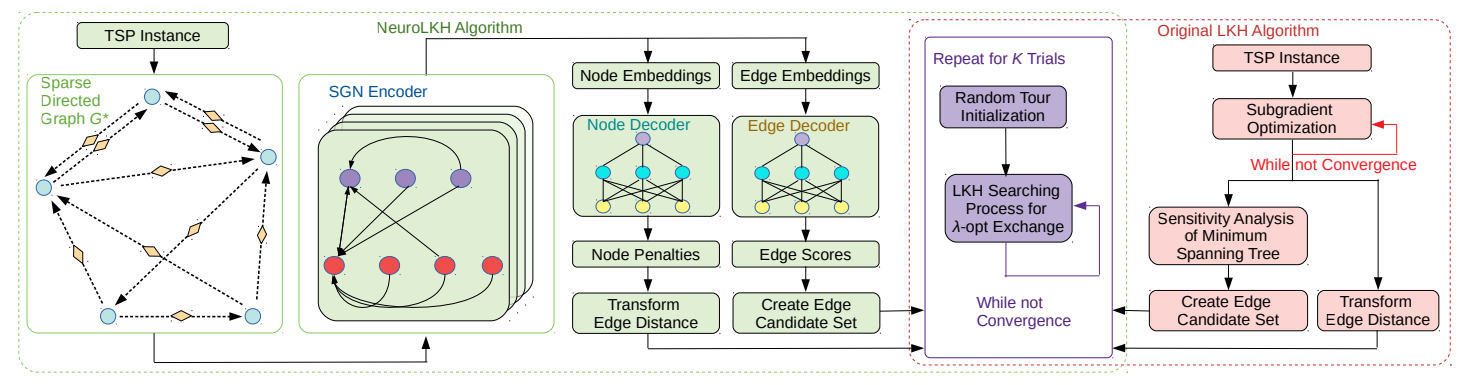
先将边和点的信息转化为特征向量，维度为，用层稀疏图卷积层来预测，实验中取和，卷积层定义为：和分别是按元素乘法和按元素除法，是层数，和都是训练的参数。

经过两层线性层后再由激活得到。同样的，经过两层线性层后再由激活得到。然后再计算和：是训练的参数，，使得范围为。

边的权值通过监督学习训练，点的惩罚通过无监督学习训练。损失函数分别为： $𝟙 𝟙$ ，即为若一条边在最优解中，则增大其权值。

为点在最小 1-tree 中的度数，为平衡两个损失函数的系数。实验中取。

对于大规模的数据，边的权值可以很好地泛化，但点的惩罚不能直接泛化。因为是通过无监督学习训练的。因此，对于进行微调，进行次迭代，批处理大小为。

图匹配

Junchi Yan, Shuang Yang, and Edwin R. Hancock. "Learning for Graph Matching and Related Combinatorial Optimization Problems.", International Joint Conference on Artificial Intelligence 5 (2020): 4988-4996.